Building a Proof of Concept Automated Market Maker in Solidity
An introduction to building a decentralized exchange
Decentralized exchanges such as Uniswap, Curve, GMX, and dYdX, have revolutionized the way people exchange assets.
There are two main approaches to building a decentralized asset exchange:
The first approach is to follow the principle of a constant product automated market maker.
Constant product automated market makers use the constant product formula to calculate how much of one asset to exchange for another. They are called “constant product” exchanges because the exchange rates of assets are determined by following a constant product rule. The simplest constant product rule is:
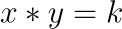
where x is the amount of token x, y is the amount of token y, and k is a constant.
They are called “automated market makers” because users who provide liquidity function as market makers, by buying and selling within a certain price range. Although they follow different architectures, Uniswap and Curve are both examples of constant product automated market makers. One of the main benefits of constant product exchanges is that users can exchange different assets without the need of finding a counterparty.
Let’s go back to the second approach. The second approach is to follow the principle of a decentralized limit order book. Given this architecture, users write to the state of the smart contract on the blockchain, then a server off-chain matches the buy order of one user to the sell order of another user. GMX and dYdX are two examples of decentralized exchanges that follow this principle.
Building a Constant Product Automated Market Maker Exchange
At their core, constant product exchanges use a mathematical formula in order to calculate how much of an asset to send to a user, given the input of another asset.
For this example, we will be building the simplest constant product exchange possible. By doing so, you will better understand the limitations of the constant product formula ***x * y = k ***and better appreciate the technical feats of projects such as Uniswap V3 and Curve.
Firstly, how do you calculate how much of token y to give in exchange for token x using the constant product formula?
Using the formula:
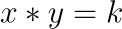
All we are saying with this formula is amount of token x multiplied by amount of token y is equal to some constant k.
We can create the following formula:
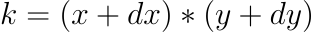
Essentially we are saying that: amount of token x plus some increment dx, multiplied by amount of token y plus some increment dy, is equal to some constant k.
Using the formula above, we can deduce that dy:

The function above tells us how much of token y we will give for a certain increment (dx) of token x.
Let’s say we have the following scenario:
A user, Bob, comes along and they want to give us 1 of token X in exchange for some amount of token Y. In our smart contract, we have 5 tokens X in our contract and 10 tokens Y in our contract (x = 5, y = 10).
This is how we calculate the amount of tokens Y to give to our user Bob in our smart contact:
uint amountOutY = (amountInX * amountY) / (amountInX + amountX);
We omit the negative sign in our code since we will be sending amountOutY to Bob.
Knowing the following, we can calculate how much of token Y to send to our user, Bob.
amountInX = 1 amountY = 10 amountX = 5
amountOutY = (1 * 10) / (1 + 5) amountOutY = 1.66
Bob sends 1 of token X and gets 1.66 of token Y in return. For Bob, this is fine, but not ideal since he experienced a slippage of 17%.
slippage = (Expected Entry Price — Actual Execution Price) / Expected Entry Price
slippage = (2–1.66) / 2
Now our smart contract has a total of 6 of tokens X and 8.33 tokens Y, meaning that the new exchange rate of token X to token Y is 1.38. Bob’s trade pushed the exchange rate of token X to token Y down from 2 to 1.38, a price drop of 31% for token X.
Let’s take another example:
Another user, Alice, wants to exchange 100 tokens X for some amount of token Y. Our smart contract contains 100,000 tokens X and 50,000 tokens Y. The current exchange rate is 0.5 tokens X for 1 token Y.
Swapping 100 tokens X yields Alice 49.95 of tokens Y. Alice experiences a slippage of less than 0.01%. Not bad for Alice. However, this is only because the size of Alice’s trade was small compared to the value deposited in the pool. The new exchange rate is 0.499 tokens X for 1 token Y.
Constant Product Function Visualized
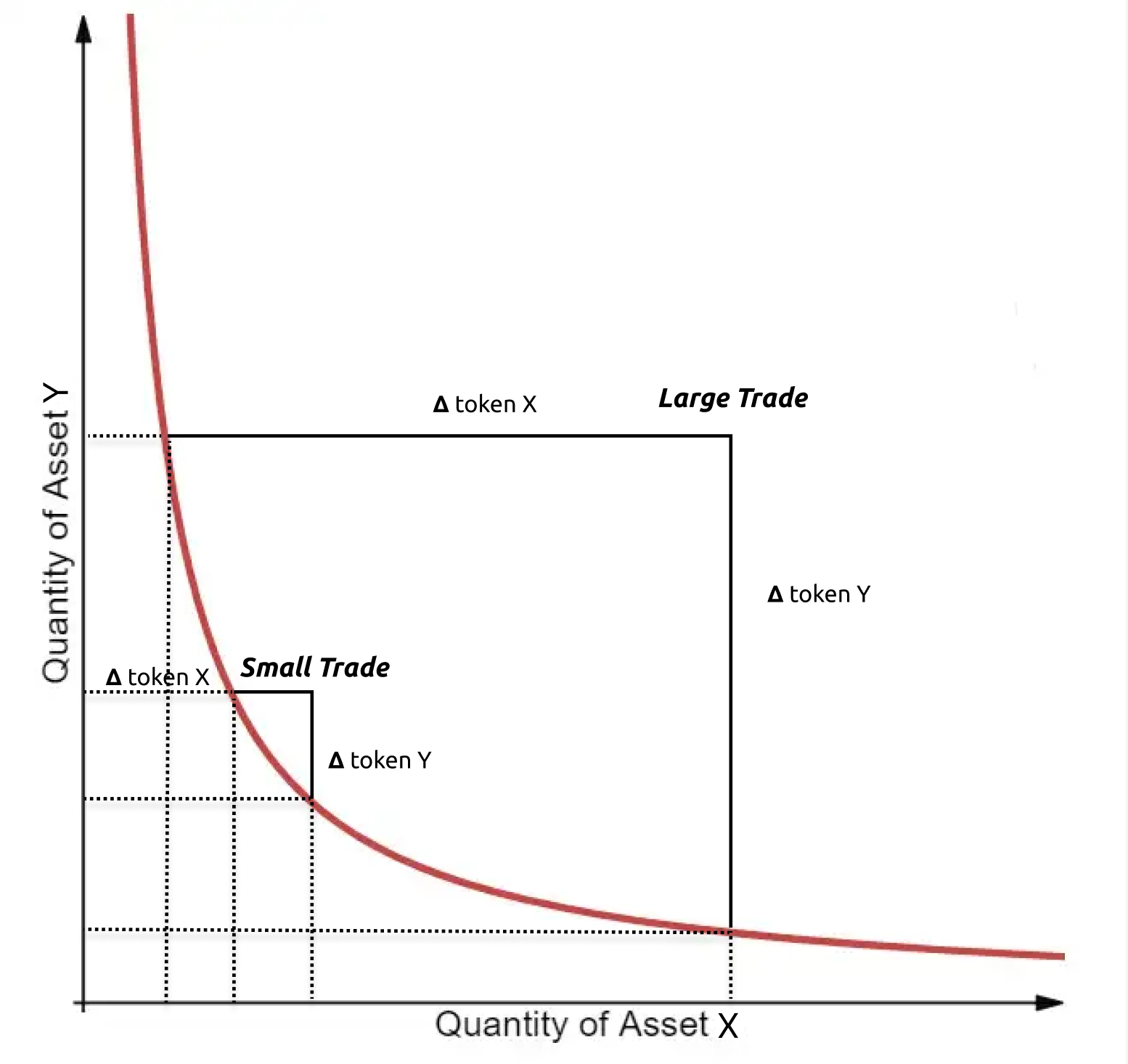
The chart above is a visualization of the constant product function that we implemented in our smart contract. As you can see, a larger change in token X results in a larger change in token Y, and vice versa.
The exchange rate in an a constant product function exchange is the ratio of tokens X to tokens Y.
Testing Our Solidity Smart Contract
To follow along, clone the simpleAMM repository from my GitHub: GitHub - partylikeits1983/simpleAMM: AMM proof of concept github.co
To run the tests you will need to have foundry installed. You can install it here: https://github.com/foundry-rs/foundry
After installing foundry and cloning the simpleAMM repository, you run the tests by typing:
forge test -vv
Impermanent Loss and Limitations of Constant Product Exchanges
Users who decide to serve as market makers by providing liquidity to a constant product exchange are exposed to what is known as impermanent loss.
Exposure to impermanent loss increases as the price of the asset at the time of deposit deviates from the current market price. Impermanent loss is only “impermanent” if the price of the asset at the time of withdrawal is equal to the price of the asset at the time of deposit. Impermanent loss is very “permanent” if the asset price at time of deposit deviates from the asset price at the time of withdrawal.
However, liquidity providers are incentivized to provide liquidity as they earn fees from the percentage of volume exchanged in the asset pair. In many ways, providing liquidity to a constant product exchange can be seen as a way of shorting volatility. If a trader expects low volatility of an asset pair in a given period, they can deposit their liquidity to a constant product exchange, and in return earn fees from the volume.
The constant product automated market maker that we built is very similar in design to Uniswap V2 since it follows the same constant product function.
One of the biggest disadvantages of Uniswap V2 is the amount of slippage experienced when exchanging assets. Uniswap V3 allows liquidity providers to select a price range in which they will function as a market maker. This feature has the added benefit of significantly decreasing slippage even on larger trades.
Concentrated Liquidity on Uniswap V3
Concentrated liquidity on Uniswap V3 leads to an interesting and very complicated math problem for liquidity providers. The smaller the price range a liquidity provider sets for a given asset pair leads to the liquidity provider earning more fees. However, the tighter the price range of a liquidity position, the more the position is exposed to potential impermanent loss.
On the surface this seems to be a classic machine learning optimization problem. However, this problem becomes more complex when you factor in the liquidity depth at each price tick in the Uniswap V3 smart contract. Additionally, it is challenging to parse historical data on liquidity depth and range per asset for different EVM chains. This problem is currently considered the cutting edge of defi research, and solving it would result in a trading strategy worth millions.
Conclusion
Constant product automated market maker exchanges have revolutionized the world of decentralized finance. In 2022, decentralized exchanges processed $788 billion in volume and had over 5.7 million users.
Although these novel exchanges still process a fraction of the volume of traditional centralized exchanges, they have proven themselves to be the cornerstone of the decentralized finance world.
I look forward to seeing future innovations of decentralized exchanges and how software engineers and researchers tackle new challenges such as mitigating impermanent loss.
What do you think about decentralized exchanges? Are they cutting-edge technology that will bring financial sovereignty to their users, or gen-z’s version of a snake oil salesman pyramid scheme?
If you liked this article, be sure to share it!
Cool and Useful Links:
Dune Analytics DEX Metrics: https://dune.com/hagaetc/dex-metrics
Uniswap Analytics: https://info.uniswap.org/
Uniswap V3 Fee Calculator: https://uniswap.fish/?network=ethereum
Impermanent Loss Desmos Calculator: https://www.desmos.com/calculator/i8h0wzqaci
Strategic Liquidity Provision in Uniswap v3: https://arxiv.org/pdf/2106.12033.pdf
Note to reader: The code snippets in this article were labeled as being javascript since medium still doesn’t have solidity as a display option.